99精品久久久久久久免费看蜜月/欧美激情做真爱牲交视频/日本不卡不码高清免费观看/三浦惠理子jux240久久 - 他在车里撞了我八次主角是谁

FM波與PM波的比較，調角波的性質

當未調載波為UC（T）=UCCOSWCT，調制信號為單音余弦UΩ（T）=UΩCOSΩT時，根據定義，FM波的瞬時角頻率W（T）應為W（T）=WC+KFUΩCOSΩT

式中KF為比例常數，表示單位調制電壓所引起的頻移（相對于載波角頻率WC）。PM波的瞬時相位φ（T）應為：φ（T）=WCT+KPUΩCOSΩT

式中KP為比例常數，表示單位調制電壓所引起的相位偏移（相對于載波相位WCT）。

FM波和PM波的比較見表5.5-4。

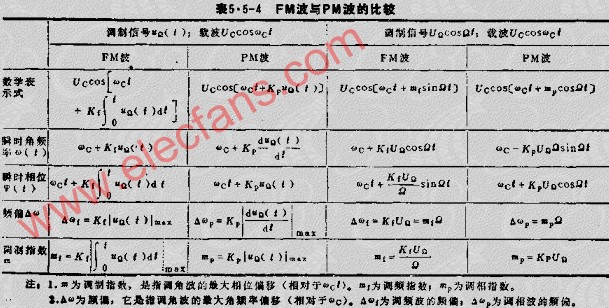
2、調角波的頻譜與帶寬（B）

由于FM波與PM波的方程相似，因此，只要分析其中一種的頻譜，則另一種也完全適用。所不同的是一個用MF，另一個用MP。

由上式可見，單音調制的FM波，載頻分量上下各有無數個邊頻分量。它們與載頻分量相隔都是調制信號角頻率Ω的整數倍。載頻分量與邊頻分量的振幅由對應的貝塞爾函數JN（M1）的值決定，并可根據不同MF值查貝塞爾函數表（見表5.5-5）得到。

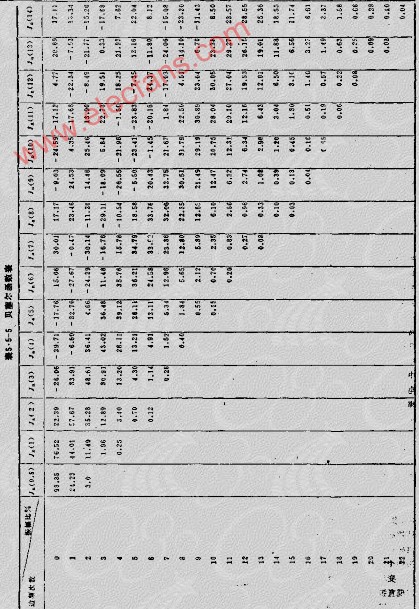
由貝塞爾函數理論證明，當N﹥（MF+1）時，FN（MF）之值就小于0.1。如果將小于未調載波振幅10%的邊頻分量忽略不計，FM波的頻帶寬度為：

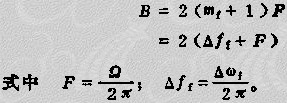
實用中，為了減小失真和干擾，FM波的通頻帶還應加寬一些，通常取：

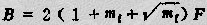
不難分析，FM波所占帶寬幾乎與F無關，這是模擬通信系統中廣泛采用FM制的重要原因之一。